El álgebra de mapas es la estrategia principal para obtener una capa de salida a partir de la combinación de múltiples capas de entrada que son procesadas por medio de una operación o algoritmo. Las estrategias de combinación y cruce de capas, en su metodología más básica, vienen de la mano de la cartografía vectorial. Las tradicionales herramientas de Intersect, Merge o Union pueden ser algunos ejemplos sencillos para trabajar el álgebra de mapas de manera básica. Pero el potencial está en la cartografía de variables continuas, trabajando con píxels y sacando la mayor riqueza de datos a lo largo de las superficies de análisis. De ahí su relevancia en el análisis de variables territoriales.
La cartografía vectorial es más propia de variables discretas que definen con precisión los límites de los elementos bajo un único valor, pero no aportan variedad de datos. Así, los límites de un espacio natural protegido responderían a una variable discreta con un solo valor constante ( como superficie, nombre, nivel de protección) a lo largo de sus límites.
La cartografía ráster es capaz de trabajar variables continuas donde, cada punto del territorio, puede estar mostrando un valor diferente. Por ejemplo, ofreciendo distintos valores de altitud a lo largo de la superficie de ese espacio natural protegido.
El álgebra de mapas no deja de ser una batidora donde incorporar datasets para obtener un resultado a través de la superposición de esas variables. Puede ayudarte a clasificar o identificar zonas territoriales que cumplan una particularidad. En medio ambiente, y trabajando con variables continuas, el álgebra de mapas, puede ser tu aliado para obtener mapas basados en:
- Zonas de reintroducción de especies
- Lugares con mayor potencial de biodiversidad
- Sectorización de zonas susceptibles a la erosión
- Zonas territoriales potencialmente inundables
- Localización de infraestructuras con menor impacto ambiental
- Distribución potencial de especies
Los operadores aritméticos (sumas, restas, divisiones, multiplicaciones…) y los operadores condicionales, son los habituales más tradicionales en la gestión de variables continuas medioambientales asociadas al álgebra de mapas. Pese a ello, el álgebra de mapas entraña ciertos rituales técnicos a seguir para evitar resultados erróneos. Detrás de la combinación de los mapas hay aspectos técnicos peligrosos que no deberías perder de vista para evitar combinar píxels de manera equívoca. Aquí tienes algunos de las premisas más peligrosas a tener en cuenta mientras trabajas con el álgebra de mapas.
Tamaño de pixel uniforme
Utilizar un tamaño de píxel adecuado durante el álgebra de mapas es fundamental para obtener resultados coherentes. El tamaño de píxel escogido debería:
- Representar el tamaño mínimo de elementos que quieres analizar o representar (por ejemplo, masas de agua perfectamente definidas)
- Representar el tamaño mínimo de la superficie objeto de análisis (por ejemplo, zonas de campeo de especies o parcelas agrícolas)
- Presentar dimensiones uniformes para todas las capas de entrada empleadas en el análisis.
Cuanto más grande sea la resolución espacial de tu pixel, menos se adaptará a los límites de elementos territoriales pudiendo distorsionar los resultados.
![]()
La excesiva desvirtuación del tamaño de pixel, además de definir incorrectamente los límites espaciales, también puede generar infravalorar o sobreestimar resultados espacialmente. Para evitar sobreestimas o infravalorar tus datos, no es apropiado combinar las variables ráster sin previamente identificar la resolución o tamaño de pixel de todas las capas a combinar. Salvo que puedas desempeñar una interpolación de píxel que permita obtener píxels más pequeños interpolando datos, deberías limitar el conjunto de capas a un único tamaño de píxel.
En caso contrario, al combinar pixels de diferentes tamaños, correrás el riesgo de infravalorar o sobreestimar datos en el resultado final.
Ausencia de dato Vs datos nulos
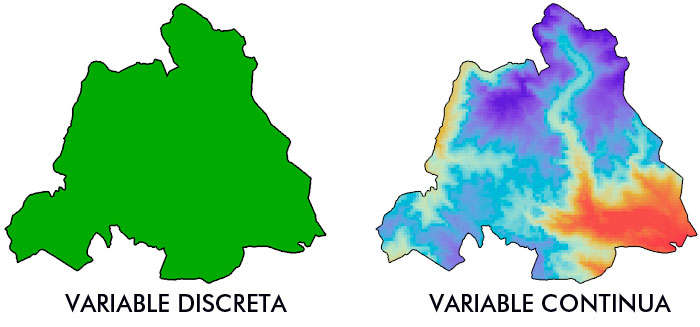
Confundir los conceptos de valores nulos y ausencia de datos es uno de los problemas más graves que puedas encontrar a la hora de meter tus variables en la batidora del álgebra de mapas. La ausencia de un dato implica que no existe información en un hipotético pixel o zona espacial. Un dato nulo indica que se conoce el valor del pixel y es igual a cero (o cualquier otro identificador numérico que lo describa como nulo). Aunque parezcan cosas iguales tienen implicaciones distintas.
La presencia de valores nulos seguirá mostrando una estructura continua de pixels asignando valores igual a cero. Por el contrario, la ausencia de datos generará huecos espaciales en tus variables. La combinación de capas con huecos durante el álgebra de mapas puede producir, en algunos casos, capas resultantes con ausencia de información, aunque existan datos parciales provenientes de otras capas.
![]()
Siempre que puedas, intentar rellenar y documentar la ausencia de información para evitar pérdidas de información en los resultados finales o infravalorar resultados durante la aplicación de los operadores que gestionarán el resultado.
Límites espaciales
De la misma forma que puedes encontrarte agujeros con ausencia de información en tus variables ambientales, también es posible que los límites espaciales no coincidan entre sí. Lo interesante del álgebra de mapas es superponer pixels de manera exacta y no dejarse ningún pixel suelto, incluidos los píxels periféricos. Estas situaciones las podrás encontrar, por ejemplo, en las periferias de los límites espaciales de tus variables, en zonas de costa o en territorios insulares.
![]()
Herramientas de recorte ráster pueden ayudarte a fijar los límites espaciales de todas las capas a través de una capa vectorial basada, por ejemplo, en unidades administrativas. Si los límites espaciales periféricos de todos los datasets no sobrepasan los límites administrativos objeto de análisis, perderás información sesgando los resultados finales en las zonas periféricas de la variable. Si los límites de tus capas sobrepasan los límites administrativos tendrás más opciones de preservar la totalidad de los píxels en cada capa.
Interpolaciones periféricas
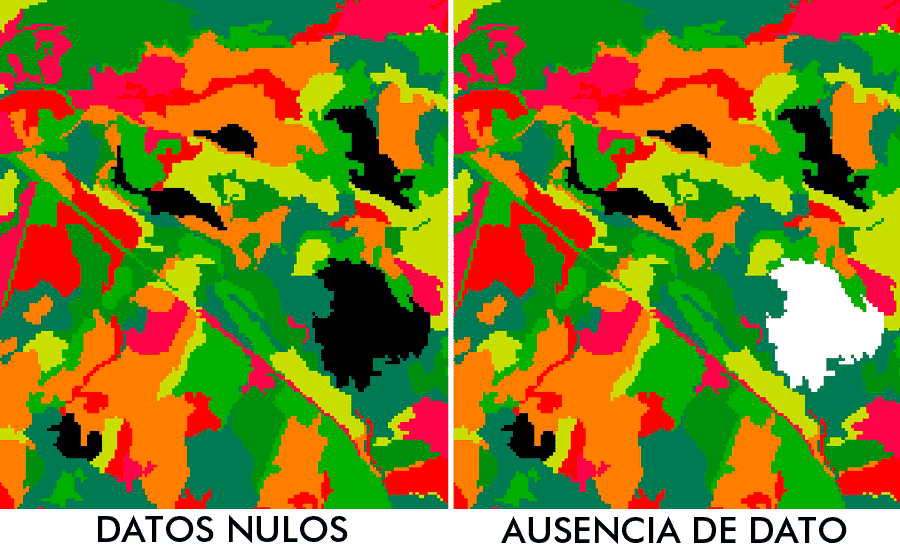
En ocasiones, información vectorial inicial basada en puntos y líneas, requiere de una interpolación para disponer de una superficie continua de píxels. Por ejemplo, si estás interpolando datos de temperatura provenientes de coordenadas de estaciones climáticas. En muchas ocasiones, estos análisis, se basan en datos de elementos obtenidos por coincidencia espacial de la zona de trabajo perdiendo información relevante peso en las zonas próximas.
Bajo este tipo de situaciones, es interesante no acotar el análisis bajo una interpolación exclusiva de elementos contenidos en los límites internos de la zona de estudio. Una interpolación basada únicamente en estos elementos hará que tus datos limítrofes en la superficie ráster se vean sesgados. Siempre es preferible contar con datos espaciales que sobrepasen los límites de la zona de trabajo, interpolarlos más allá de suslímites y, posteriormente, realizar recortes empleando los límites de la zona AOI de estudio.
Centrado de pixel
Las técnicas de conversión de cartografía vectorial a ráster te ayudarán a rasterizar los datos vectoriales. Pero no despistes, durante la conversión de vector a ráster, que los píxel de todos los datasets se encuentren alineados bajo una rejilla común.
El desplazamiento de píxel entre variables puede producir desviaciones de valores finales en el proceso de superposición de píxel del álgebra de mapas. Algunas aplicaciones de análisis ráster no permiten la superposición de ráster cuyos pixels no solapen y coincidan espacialmente entre sí.
![]()
La alineación de píxels parte, en muchas ocasiones, por evitar desplazamientos de capas. Y uno de los grandes motivos de estos desplazamientos lo encontrarás en el tema de las proyecciones. Intenta ser cuidadoso con los desplazamientos y empieza gestionando las capas y sus sistemas de referencia de manera correcta.
Profundidad de píxel
Presta mucha atención a la hora de gestionar el resultado de la suma u operación entre capas. La capa resultante debería disponer de una naturaleza de píxel que permita albergar el valor resultante final con una amplitud de valores adecuada según su profundidad de pixel. Aunque no lo creas, asignar erróneamente una naturaleza de píxel basada en un número entero o un número decimal puede hacer variar los resultados y redondear la información infravalorando o sobreestimando los resultados finales.
Ten en cuenta las naturalezas de píxel de todas y cada una de las capas que estás empleando, pero más aún el de la capa resultante para disponer de un resultado preciso. El formato de archivo ráster de salida limitará la posibilidad de incorporar más o menos repertorio de valores y que tu capa resultante ocupe más o menos peso.
![]()
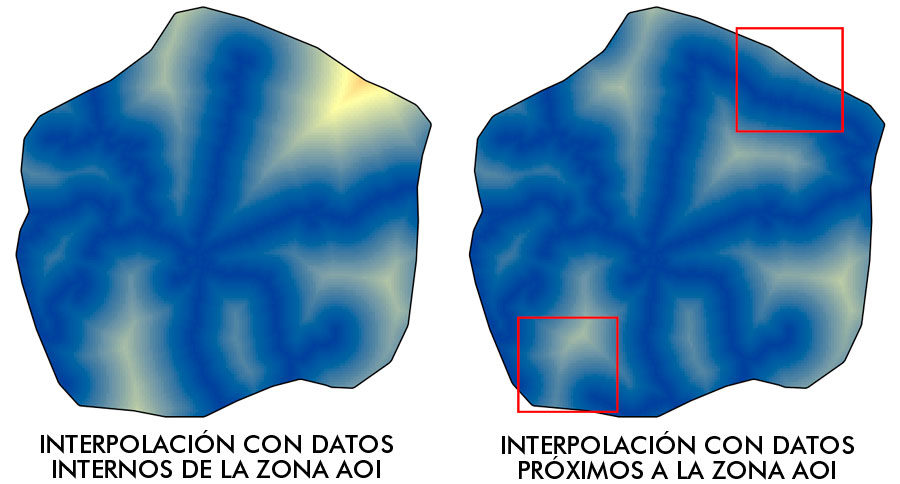
Interpretación de resultados
Si realizar un adecuado análisis con álgebra de mapas es fundamental en tus mapas, exportar resultados interpretables lo será aún más. Si tus valores van a ser interpretados visualmente por colores, el formato de archivo limitará los tonos de color. Y aunque el ojo humano no es capaz de identificar un repertorio cromático amplio, el formato de archivo que escojas para la salida podrá condicionar que algunos colores se equiparen entre sí sesgando el resultado, especialmente en formatos de archivo web como el GIF. En función de la profundidad de pixel empleada, aquí tienes algunos formatos de archivo ráster a emplear.